建構具有信心程度的仿真基因調控網路模型
本核心交通大學生物資訊及系統生物研究所何信瑩教授所帶領的研究團隊,目前發展了一套建構仿真基因調控網路(emulated gene regulatory network, eGRN)模型的演算法GREMA,在給定實驗的基因量測數據不充足時,能夠解決所導致的求解數學模型不唯一解的欠定問題(underdetermined problem),所解出的每一條調控關係具有促進或抑制的方向性、調控強度的定量值和準確度相關的信心程度指標。簡言之就是使用少量的基因量測數據而能建構相對較準確地仿真基因調控網路模型。GREMA演算法已經投稿Bioinformatics期刊(第二次審核中)[1],本文將對此演算法目前的研究成果與提供服務做一簡介。
一、基因調控網路建模演算法
生物系統中細胞作用過程的基礎行為模型是不易化簡且非線性的系統。包含所有調控相互作用的基因調控網絡(GRN)的數學模型可以幫助理解網絡拓撲,功能機制以及對GRN行為的預測[2]。具有大量參數基於非線性常微分方程(ordinary differential equation)的模型適用於推論eGRN以便研究真實的GRN。eGRN的模型參數數量通常比會導致不唯一解的欠定問題的實驗測量數據量大得多[3]。欠定問題是存在多個候選GRN模型,這些候選解的模型都可以模擬基因表現圖譜,且和真實圖譜的誤差一樣好,但其中只有少數是真實存在的基因調控網絡,這是重建eGRN模型的當前瓶頸[4]。
最新的非線性ODE模型主要有兩種:S-system模型和基於Hill函數的ODE模型(HFODE)[5]。兩種類型的模型都被認為適用於表徵生化網絡系統和分析監管系統動態。S-system模型可以推斷網絡的拓撲結構[6]。HFODE模型可以推斷拓撲和調節特性的其他動力學參數,例如轉錄因子及其結合位點之間的化學親和力。HFODE模型參數的數量通常大於其他非線性ODE模型的參數數量。
根據其推論的基因調控關係,GRN可以分為三種類型:無方向性、具方向性和定量GRN (Fig.1)。無方向GRN的調控關係僅以節點之間的相關性或依賴關係的形式表示,而沒有揭示這種關係的原因[7](Fig.1A)。對於具方向GRN,在表達模式內觀察到的兩個節點之間的相關性是由一個與調節標靶基因的轉錄因子相對應的節點引起,例如是促進或抑制關係(Fig.1B)。對於定量GRN,可以對調控關係進行特徵描述和量化。推論定量GRN的方法,在Fig.1C中,關係的線粗度表示調控強度。
在實際使用時很難獲得足夠的實驗數據量來推論eGRN模型。通常使用特定假設和簡化來處理欠定問題以便推論GRN模型。一種廣泛使用的策略是將非線性模型簡化為線性模型[8]。但是簡化模型會缺少有關基因調控相互作用的一些生物學訊息。處理有限數量數據點的另一種策略是從實際/模擬時間序列的基因表現譜(expression profile)產生成多個模擬時間序列表現譜,以推論非線性模型的GRN。使用多個模擬時間序列表現譜的方法包括Time-Delayed S-system[9],合作進化模型[10]和智能兩階段演化演算法[11]。
本研究提出了一種演化建模演算法(evolutionary modelling algorithm, EMA)來解決欠定問題,並提出了一種基於EMA稱為GREMA的方法來推論一種新型態的GRN,這是一種具有信心程度的定量GRN(Fig.1D)。GREMA使用S-system或HFODE模型來推論eGRN,而無需增加使用多個模擬時間序列表現譜。GREMA採用動態式推論基因調控關係,對基因表現譜影響力較大且推論較準確的調控關係會先決定出來,這時我們付予較高的信心程度;愈晚決定出來的調控關係其影響力較小且推論的準確度較低,此時付予較低的信心程度。當要建模的實驗數據量增加到充分時,所有推論的每條調控關係其信心程度都很高,即準確度很高,也就是可得到正確的eGRN模型。我們使用多個測試標準數據集對GREMA進行評估,包括著名的DREAM4 challenge,S-system和SOS DNA repair system數據集。
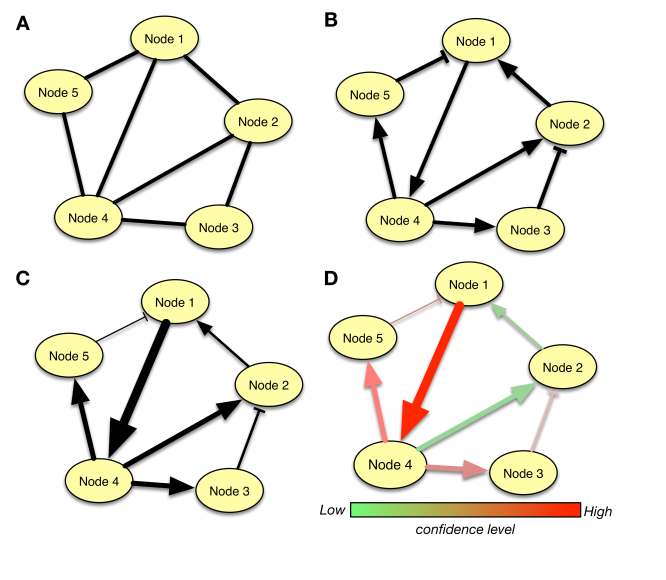
Fig 1. The four types of GRNs. (A) Undirected GRN; (B) Directed GRN; (C) Quantitative GRN; (D) Quantitative GRN with confidence levels (proposed in this work). [1]
二、基於演化智慧的演算法GREMA
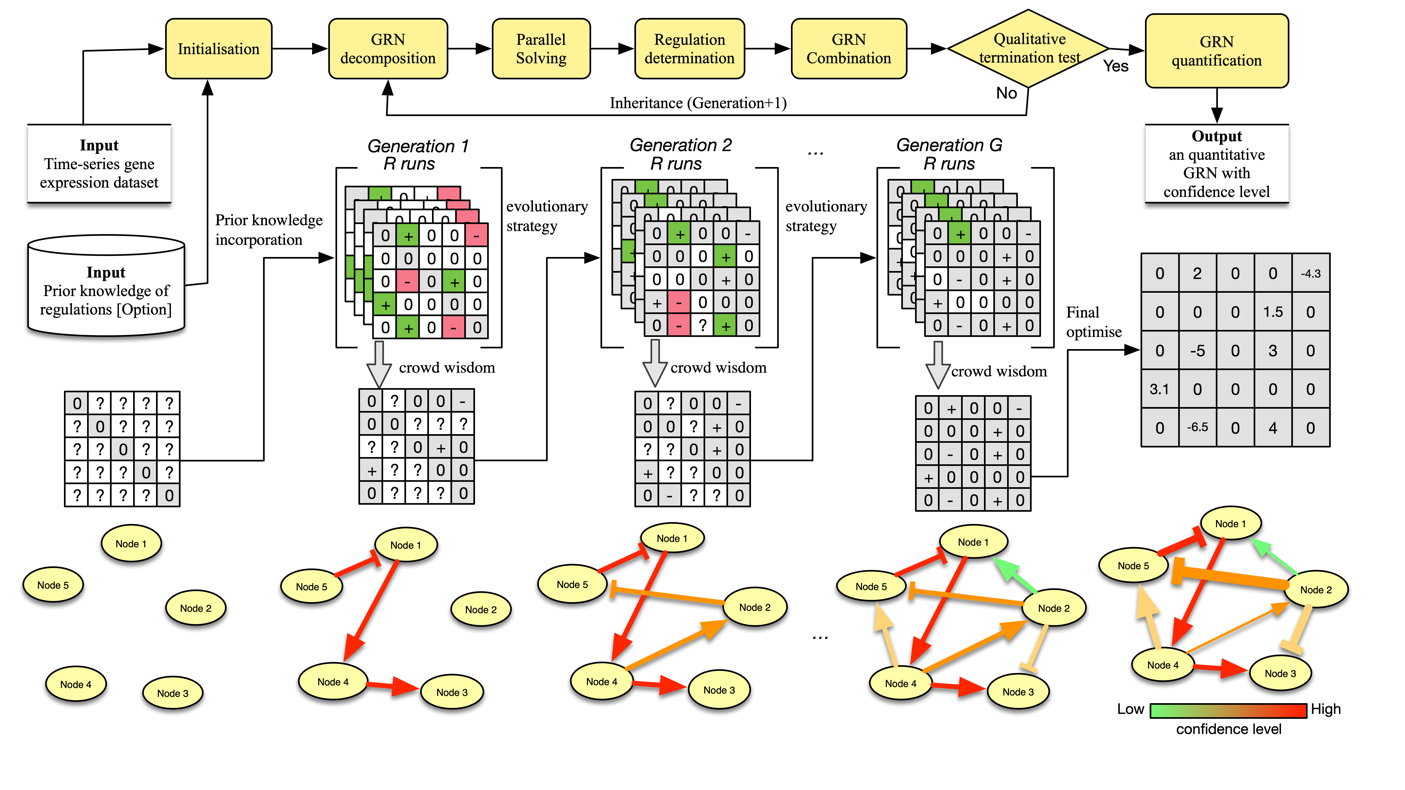
GREMA利用了演化智慧(evolutionary intelligence),包括群體智慧(crowd wisdom)和演化策略(evolutionary strategy) 來建立具有大量系統參數的非線性常微分方程模型。群體智慧的概念是產生多組候選解模型,其中正確的調控關係會穩定出現,不怕雜訊干擾,所謂真金不怕火,因此可以用多數決投票方式決定。另一方面,演化策略利用物競天擇、適者生存的原則,所有調控關係包含方向、強度、信心程度等經由不斷演化,達到最佳模型的建立。
GREMA的輸入為time-series profiles,演算法大致可分為9個步驟(Fig.2):1)初始化,尚未決定任何調控關係,2)GRN分解,把N節點的GRN推論問題分解成N個1節點的GRN推論問題,3)平行求解1節點的GRN推論問題,4)以多數決投票決定出可確定的調控關係,5)GRN組合N個1節點的GRN模型,6)終止測試,看是否所有調控關係都已經確定,若是則跳到步驟8,7)繼承已經確定的調控關係後繼續演化,即回到步驟2,8)GRN量化,此時已完全確認調控關係,進行調控強度數值的優化,9)輸出eGRM和每一條調控關係的信心程度。 Fig.2顯示了演化智慧的過程,灰色方框代表確定的調控關係,白色方框代表尚未確定的調控關係,綠色方框代表促進的調控關係,紅色方框代表抑制的調控關係,節點之間的調控關係顏色代表信心程度。經由多個標準測試集的效能評估和比較,GREMA可以獲得滿意的成果,包含正確性、信心程度的驗證和執行時間等。
三、建立仿真基因調控網路模型的研究服務
本研究團隊已發展出多種型態的基因調控網路演算法[1,8,11],本核心提供基因調控網路數學建模的客製化研究服務。
參考文獻
[1] M-J Tsai, J-R Wang, S-J Ho, L-S Shu, W-L Huang and S-Y Ho*, GREMA: Modelling of emulated gene regulatory networks with confidence levels based on evolutionary intelligence to cope with the underdetermined problem, submitted to Bioinformatics 2020 (under revision).
[2] Marbach, D., et al. Generating realistic in silico gene networks for performance assessment of reverse engineering methods. J Comput Biol 2009;16(2):229-239.
[3] Ud-Dean, S.M. and Gunawan, R. Optimal design of gene knockout experiments for gene regulatory network inference. Bioinformatics 2016;32(6):875-883.
[4] De Smet, R. and Marchal, K. Advantages and limitations of current network inference methods. Nat Rev Microbiol 2010;8(10):717-729.
[5] Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits. Chapman and Hall/CRC; 2006.
[6] Vilela, M., et al. Parameter optimization in S-system models. BMC Systems Biology 2008;2.
[7] Barabási, A.-L. and Oltvai, Z.N. Network biology: understanding the cell's functional organization. Nature Reviews Genetics 2004;5:101.
[8] Chen, Y.H., et al. GeNOSA: inferring and experimentally supporting quantitative gene regulatory networks in prokaryotes. Bioinformatics 2015;31(13):2151-2158.
[9] Chowdhury, A.R., Chetty, M. and Vinh, N.X. Incorporating time-delays in S-System model for reverse engineering genetic networks. Bmc Bioinformatics 2013;14.
[10] Kimura, S., et al. Inference of S-system models of genetic networks using a cooperative coevolutionary algorithm. Bioinformatics 2005;21(7):1154-1163.
[11] Ho, S.Y., et al. An intelligent two-stage evolutionary algorithm for dynamic pathway identification from gene expression profiles. Ieee Acm T Comput Bi 2007;4(4):648-660.